18-March-2010
Insulating refractories are thermal barriers that keep in the heat and save energy.
Furnaces used for melting, heat treatment, heat regeneration or for any other purpose demand maximum heat conservation so as to minimize heat losses for maximum heat efficiencies and minimum fuel consumption as well as high production as a result of maintaining high working temperatures. As the cost of energy has increased, the role of insulating refractories has become more important. Not too long ago, energy costs were low and stable, while the costs of insulating materials and, particularly, installation labour were moving northwards. Those circumstances dictated the use of minimal insulation. The situation is quite different now. The use of considerable quantity of refractories is socially and economically justified. With today’s energy costs at such higher levels has come the development of a wide range of new insulating refractory materials and technology of high-temperature insulation which are capable to restrict the escape of heat even at a much elevated temperature. Instead of going direct into the discussion of insulating refractories, their types, raw materials, manufacturing, properties and applications etc., here we will first review some of the fundamental technology of high-temperature insulation.
Insulating refractories are thermal barriers that keep in the heat and save energy.
Furnaces used for melting, heat treatment, heat regeneration or for any other purpose demand maximum heat conservation so as to minimize heat losses for maximum heat efficiencies and minimum fuel consumption as well as high production as a result of maintaining high working temperatures. As the cost of energy has increased, the role of insulating refractories has become more important. Not too long ago, energy costs were low and stable, while the costs of insulating materials and, particularly, installation labour were moving northwards. Those circumstances dictated the use of minimal insulation. The situation is quite different now. The use of considerable quantity of refractories is socially and economically justified. With today’s energy costs at such higher levels has come the development of a wide range of new insulating refractory materials and technology of high-temperature insulation which are capable to restrict the escape of heat even at a much elevated temperature. Instead of going direct into the discussion of insulating refractories, their types, raw materials, manufacturing, properties and applications etc., here we will first review some of the fundamental technology of high-temperature insulation.
The function of insulating refractory is to reduce the rate of heat flow (heat loss). Although it is not possible to totally prevent the flow of heat energy when there exists a temperature differential between two points, but it can be retarded. There are three mechanisms of heat transfer that we must understand. These are conduction, convection, and radiation. We must consider all these three mechanisms when we study the overall conductivity of a given material.
Heat transfer by Conduction occurs via the transfer of energy from atom to atom (or molecule to molecule) in a material. Atoms vibrate faster in higher temperature as they possess more energy. This energy will be passed to the adjacent atoms having lower energy. Since atoms and solids are bonded to one another and are in close contact, conduction in solids is higher than in liquids. Metals, especially, have high rates of conduction because both the atoms and their electrons conduct the electrons much more rapidly. Liquids generally have lower conduction rates than solids because of their lack of regular structure and strong bonding. Gases have much lower rates of conduction since their molecules exist at much lower concentrations and are in relatively infrequent contact. So, within metals, dense ceramics, and dense refractories Conductivity is the main mechanism of heat transfer.
Energy transfer by Convection relies on the mass movement of a fluid. The moving fluid may be either a liquid or a gas. Convection does occur horizontally; but it depends on the gravitational force of the earth. Again, in case of dense refractory bricks heat transfer through this process can not happen since there is no fluid for convection.
Radiation process of heat transfer does not require the presence of any material. Radiation occurs most readily through empty space. The sun radiates energy through space to earth. Similarly all hot bodies radiate heat, and if they are hot enough they also radiate visible light which we call as glow.
When one studies heat transfer mechanisms in industrial processes, all three modes of heat (or energy) transfer must be considered. In a high temperature furnace or kiln, for example, energy is transferred from the heat source i.e. a burner to the material being heated and to the surrounding furnace refractory walls by all the three processes. The amount of energy transferred by radiation increases dramatically as the temperature increases. It is the dominant heat transfer mechanism at high temperatures. The load and the refractories of the furnace wall absorb energy, get hot, and re-radiate energy. The moving gases within the carry heat with them and transfer it when they come in contact with cooler solid. A small amount of gas conduction occurs, and conduction is the main process of transferring energy or heat from the surface of the solid or liquid load to its own interior.
One of the prime roles of a refractory is to withstand the effects of heat usually in a hostile environment. That is why for the selection of refractory and its designing Thermal Conductivity is one property which one has to consider. Usually one would like to have a refractory with low thermal conductivity so that heat may be more effectively contained within a furnace or kiln. Sometimes, however refractories and materials having high thermal conductivity are desired. For example, a protective muffle in certain ceramic kilns is designed to prevent combustion gases from reaching the ceramic ware. It must transfer as much heat to the ware as possible, so conductive ceramic materials like silicon carbide are often used for muffles.
Since insulation refractories find application in processes involving thermal energy, an understanding of thermal properties especially, thermal conductivity of these refractories is quite important. Thermal Conductivity of a refractory material, k, is a measure of the amount of heat that it will allow to pass under certain conditions. Thermal conductivity can be defined as the quantity of heat transmitted through a material in unit time, per unit temperature gradient along the direction of flow and unit cross sectional area. First, let us understand the material conditions affecting this thermal property of a refractory brick whether it is insulating or normal brick, and then the most common method used to measure (or calculate) the same. While there are many factors affecting the thermal conductivity of refractories, some of the most important are [Reference: J.E. Burke, Progress in Ceramic Science, Vol. 2, Ed., Pergamon Press, Chapter 4, 1962]:
1. Temperature
2. Complexity of structure (crystal and microstructure)
3. Defects (impurities, solid-solution, and stoichiometry)
Fig: Temperature dependence of thermal conductivity for several materials
The temperature dependence of thermal conductivity of several materials is shown in the adjacent figure. In general, the thermal conductivity is expected to decrease with increasing temperature when the temperature exceeds the Debye temperature. The Debye temperature is a characteristic temperature for a given material and may be below or above room temperature. The structural features such as, anisotropic arrangement of ions, relative mass difference between anion and cation, pores, and grain boundaries etc. do affect thermal conductivity of a material. Spinel (MgAl2O4) for instance, has a thermal conductivity lower than that for either MgO or Al2O3. Another example is reducing the thermal conductivity of a solid by introducing porosity and this is the most common technique of manufacturing insulating refractories.
Fortunately for us, the thermal conductivity of a refractory material is ordinarily measured in such a way as to account for all of the heat transfer processes that happen to be operating in that material. We do not have to unscramble them or deal with tem separately, for most ordinary purposes. Once that property is known for each material in the vessel, some very sophisticated calculations can be performed to find out where the heat goes in a given operation.
In the next following lines we will discuss only the simplest of these calculations. This will be enough to enable you or someone to select among various insulating refractories and also to measure what will be the refractory lining thickness.
In the next following lines we will discuss only the simplest of these calculations. This will be enough to enable you or someone to select among various insulating refractories and also to measure what will be the refractory lining thickness.
Imagine a large flat slab or wall of refractory, whose hot face (hot side), is at some fixed temperature, Th. Its cold face (cold side) perhaps in contact with a steel shell, is at some lower temperature, Tc. We will call the thickness of the refractory X. Let us assume that the heat is supplied to the hot face at some fixed rate by process fluids, and that heat is removed from the cold face (may be by the steel shell and the air outside it) at exactly the same rate. Two things then follow: (a) heat flows through the refractory at exactly the same rate as well and (b) temperatures Th and Tc do not change with time. This is called Steady State situation. If we call some amount of heat H flows in time interval t then the rate of heat-flow Q would be H / t. If you think about it, you will understand that this rate of heat-flow or heat transport has to be proportional to the area of refractory wall, A, through which heat is flowing. One mathematical equation connects all of these things at once is:
where, k is the value of thermal conductivity.
To use this equation, we will adopt a set of English units that engineers in the fields of processing and refractories are familiar with. The unit of heat energy, the BTU (British thermal unit), is defined as the amount of heat that will raise the temperature of 1 pound of water by exactly 1OF. The unit of time will be hour (hr). We shall take units of area A in square feet (ft2), the thickness X in inches (in.) and temperature in OF. Clearly if the situation described by A, X, Th, and Tc is held fixed but different materials are studied, the rate of heat transport (Q or H/t) will be proportional to the k (thermal conductivity) of each material. Since k is a property of each material, we can get different values for the rate of heat transport by choosing different materials or mixtures of them. Thermal conductivities i.e. values of k for different materials are measured in the laboratory and published. We can use them in calculations with the above equation. Only we need to make sure that the units of k are (BTU.in)/(ft2.OF.hr).
In fact, k is numerically equal to the rate of heat transport when the slab area (here, area of the refractory or furnace wall) is exactly 1 ft2 and the temperature gradient is exactly 1OF/in. The table below lists some of the typical values of thermal conductivity (k) for different solid materials: some metals, some ordinary “working” refractories, some insulating and some highly conducting refractories. Given below are some examples of how to calculate Heat Loss or Heat Transport and Thickness of Refractory Lining:
Suppose we have a furnace lined with Superduty refractory brick, and the total wall area of this furnace is 1350 ft2 and also suppose the refractory lining thickness is 12 inch. Say, the process we are conducting in this furnace keeps its hot-face temperature at 3000OF. With thermocouples we find that the cold-face is at a steady temperature 600OF. Then, what will be the rate of heat loss through all the walls of this furnace ?
We find from the table given below that k for Superduty brick is 9.5. Then by putting all the given numbers into our heat transfer equation mentioned above we get the rate of heat flow (heat loss) Q as per -
It will be instructive to check here as how much less refractory it would take to match this heat loss keeping all the conditions same if we used, say, an insulating refractory firebrick whose thermal conductivity (k) value is 3.0, also taken from the table below. Suppose that this insulating brick can survive at 3000OF, to make the question reasonable. Here we will find out the required thickness of the insulating brick lining for which we first rearrange the heat transfer equation to be explicit in X so that we can solve it for the refractory thickness. Then by putting all the given numbers into the equation except 3.0 for k, we get -
That is 3.8 inch of insulating firebrick has the same heat transfer resistance as 12 inch of conventional Superduty refractory firebrick ! We would be naïve to replace the one refractory by the other until we learn more; but the effectiveness of insulating refractories in containing heat is impressive. If we were to keep the refractory lining thickness at 12 in. for example, and solve our heat transfer equation with k = 3.0, we would find that the total rate of heat loss is only 810,000 BTU/hr., instead of 2,565,000 BTU/hr. Now imagine how much thousands of dollars we could save per month in fuel costs !
However, on practical ground or real - life, calculations are never this simple for numerous reasons. For one thing, the value of thermal conductivity itself changes with temperature as the relative contributions of conduction, convection and radiation change. The second complication we will mention here is that in most cases the refractory lining of a furnace or kiln is done with several refractory layers of varying qualities:
1. A working face of refractory layer or, interior layer of refractory lining that is exposed to the process;
2. The refractory lining between the furnace or kiln shell and working lining, often referred to as the Safety Lining or Insulating Lining. Insulating linings are used to limit heat loss and to maintain the vessel (furnace) shell temperatures at reasonable levels.
Such refractory lining arrangements definitely complicate the heat transfer calculations. But even with the simple introduction about insulating refractories what we have given above, you can appreciate that a process operator can intelligently design a refractory lining that will endure its use temperature and chemistry, and at the same time meet the restrictions on refractory lining thickness or on heat loss that are specified for the situation.
In our next post Insulating Refractories (Part - II) we will look at the different types of insulating refractories and their manufacturing etc.
Table : Typical Thermal Conductivity Values
Refractories / Materials
|
k (BTU.in/ft2.OF.hr)
|
Metals (dense solid)
Copper
Aluminium
Gold
Silver
304 Stainless Steel
310 Stainless Steel
1020 Carbon Steel
|
2500
900 - 1500
2060
2900
113
96
360
|
Dense Refractories
Silica Brick
Superduty Brick
Periclase
High Alumina
Chrome - magnesite
Zirconia
|
13
9.5
20 - 50
10 - 40
14
5
|
Insulating Refractories
Insulating firebrick 2800
Insulating firebrick 2600
Insulating firebrick 2300
Ceramic Fiber Blanket 4 pcf (lb/ft3)
Ceramic Fiber Blanket 8 pcf (lb/ft3)
Vacuum formed board
Backup insulation
|
2.5 - 3.0
2.0 - 2.5
0.9 - 1.3
0.6 - 3.0
0.35 - 2.0
0.4 - 1.5
0.3 - 1.0
|
Conducting Refractories
Silicon Carbide
Baked Carbon
Graphite
|
100 - 200
300 - 800
500 - 1200
|









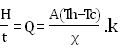
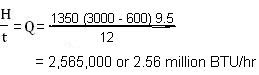
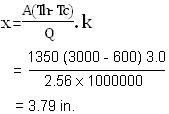
0 on: "Insulating Refractories (Part - I)"